本文共 2089 字,大约阅读时间需要 6 分钟。
机器学习算法
广泛地说,有三种类型的机器学习算法。
1.监督学习
这个算法由一个目标/结果变量(或因变量)组成,这个变量可以从一组给定的预测变量(独立变量)中预测出来。 使用这些变量,我们生成一个将输入映射到所需输出的函数。 训练过程一直持续到模型达到训练数据所需的准确度。 监督学习的例子:回归,决策树,随机森林,KNN,逻辑回归等。
2.无监督学习
在这个算法中,我们没有任何目标或结果变量来预测/估计。 用于不同群体的群体聚类,广泛用于不同群体的消费者细分进行具体干预。 无监督学习的例子:Apriori算法,K-means。
3.强化学习:
使用这种算法,机器被训练做出特定的决定。 它是这样工作的:机器暴露在一个环境中,它使用反复试验不断地训练自己。 这台机器从过去的经验中学习,并试图捕捉最好的知识,做出准确的业务决策。 强化学习实例:马尔可夫决策过程
- 这里是常用的机器学习算法列表。 这些算法可以应用于几乎所有的数据问题:
线性回归
Logistic回归 决策树 SVM 朴素贝叶斯 KNN K均值 随机森林 维度降低算法 梯度提升算法 GBM XGBoost LightGBM CatBoost
1.线性回归
它用于根据连续变量估计实际值(房屋成本,通话次数,总销售额等)。在这里,我们通过拟合最佳线来建立独立和因变量之间的关系。该最佳拟合线被称为回归线,并由线性方程Y = a * X + b表示。
理解线性回归的最好方法是重温童年的这种体验。让我们说,你问一个五年级的孩子,通过增加体重的顺序来安排班上的人,而不要问他们的重量!你觉得孩子会做什么?他/她可能会查看(视觉分析)人的身高和身材,并使用这些可见参数的组合进行排列。这是现实生活中的线性回归!实际上,孩子已经找到了身高,身材与体重之间的关系,看起来像上面的方程式。
在这个等式中:
Y因变量
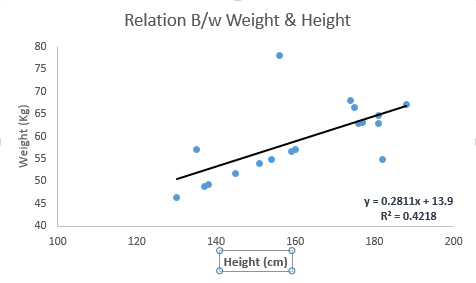
一个 - 坡度 X - 自变量 b - 拦截 这些系数a和b是基于最小化数据点与回归线之间的距离的平方和的总和而得出的。看下面的例子。这里我们已经确定了具有线性方程y = 0.2811x + 13.9的最佳拟合线。现在使用这个等式,我们可以找到重量,知道一个人的身高。
R代码:
#Load Train and Test datasets#Identify feature and response variable(s) and values must be numeric and numpy arraysx_train <- input_variables_values_training_datasetsy_train <- target_variables_values_training_datasetsx_test <- input_variables_values_test_datasetsx <- cbind(x_train,y_train)# Train the model using the training sets and check scorelinear <- lm(y_train ~ ., data = x)summary(linear)#Predict Outputpredicted= predict(linear,x_test)
python:
#Import Library#Import other necessary libraries like pandas, numpy...from sklearn import linear_model#Load Train and Test datasets#Identify feature and response variable(s) and values must be numeric and numpy arraysx_train=input_variables_values_training_datasetsy_train=target_variables_values_training_datasetsx_test=input_variables_values_test_datasets# Create linear regression objectlinear = linear_model.LinearRegression()# Train the model using the training sets and check scorelinear.fit(x_train, y_train)linear.score(x_train, y_train)#Equation coefficient and Interceptprint('Coefficient: \n', linear.coef_)print('Intercept: \n', linear.intercept_)#Predict Outputpredicted= linear.predict(x_test) 转载地址:http://dlkwo.baihongyu.com/